题目描述
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
Example1:
Input:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Output: 4
解题思路
- 参考 博客
- 使用DP。设这个DP[i][j]数组为以i, j位置为右下角顶点的能够成的最大正方形的边长。
- 初始化部分,当是第0行或者第0列的时候,根据具体的数字进行初始化
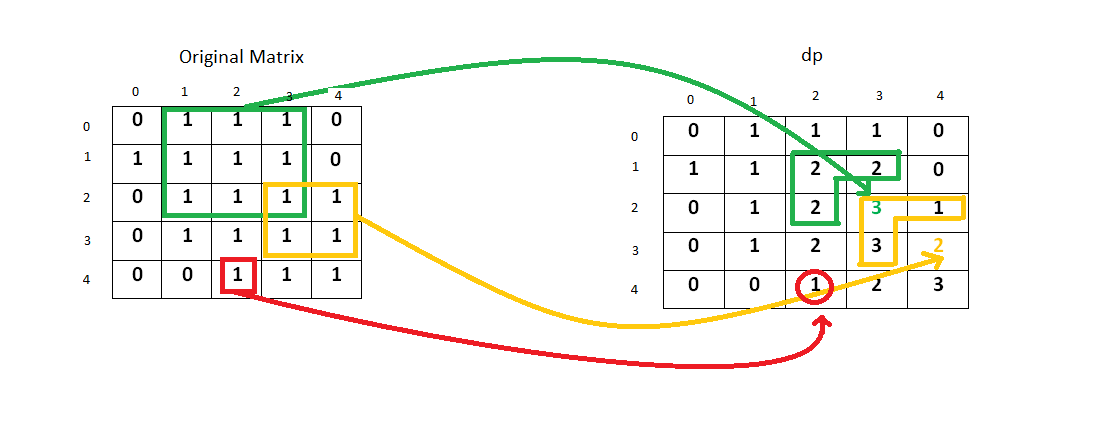
- 如果是其他位置,当matrix[i][j] = 1时,能够成的正方形等于左边、上边、左上能够成的正方形边长的最小值+1.为什么是最小值?因为只要存在一个0,那么就没法构成更大的正方形,这个是很保守的策略。
- 如图
-
即递推公式如下:
dp[0][j] = matrix[0][j] (topmost row);
dp[i][0] = matrix[i][0] (leftmost column);
For i > 0 and j > 0: if matrix[i][j] = 0, dp[i][j] = 0; if matrix[i][j] = 1, dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1.
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if(matrix.size() == 0 || matrix[0].size() == 0){
return 0;
}
int res = 0;
vector<vector<int>> dp(matrix.size(), vector<int>(matrix[0].size(), 0));
for(int i = 0; i < matrix.size(); i++){
for(int j = 0; j < matrix[0].size(); j++){
if(i == 0 || j == 0){
dp[i][j] = matrix[i][j] - '0';
}else if(matrix[i][j] == '1'){
dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
}
res = max(res, dp[i][j]);
}
}
return res * res;
}
};