题目描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。 为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
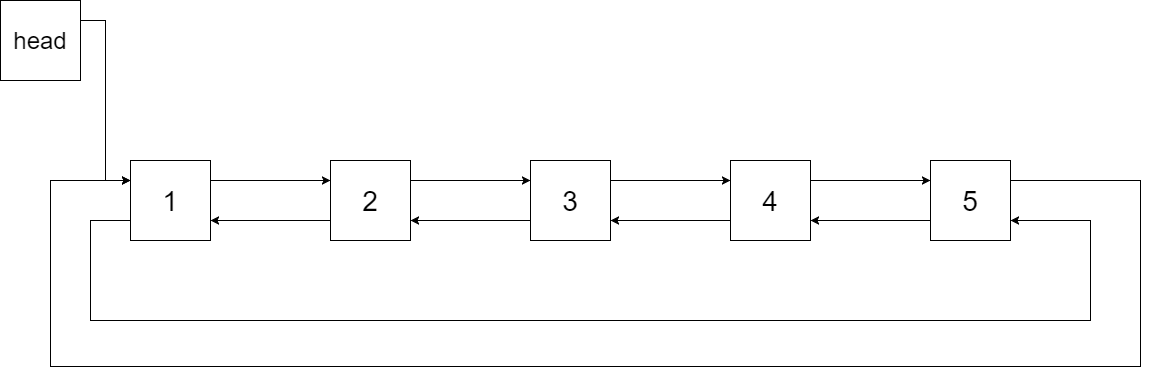
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
解题思路
- 中序遍历
- 排序链表: 节点应从小到大排序,因此应使用 中序遍历 “从小到大”访问树的节点;
- 双向链表: 在构建相邻节点(设前驱节点 prepre ,当前节点 curcur )关系时,不仅应 pre.right = curpre.right=cur ,也应 cur.left = precur.left=pre 。
- 循环链表: 设链表头节点 headhead 和尾节点 tailtail ,则应构建 head.left = tailhead.left=tail 和 tail.right = headtail.right=head 。
class Solution {
public:
Node* head; // 这里因为子函数需要对head,tail进行修改
Node* tail;
Node* treeToDoublyList(Node* root) {
if(!root) return nullptr;
helper(root);
head -> left = tail; // 循环链表
tail -> right = head;
return head;
}
void helper(Node* root) {
if(!root) return;
helper(root->left);
if(!head) {
head = root; // 找到head
tail = root; // 对pre进行初始化
} else {
tail -> right = root;
root -> left = tail;
tail = root;
}
helper(root->right);
}
};
借助vector辅助数组
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
public:
vector<Node*> v;
void helper(Node* root){
if(root != nullptr){
helper(root -> left);
v.push_back(root);
helper(root -> right);
}
}
Node* treeToDoublyList(Node* root) {
if(root == nullptr){
return nullptr;
}
helper(root);
for(int i = 0; i < v.size() - 1; i ++){
v[i] -> right = v[i + 1];
v[i + 1] -> left = v[i];
}
v[0] -> left = v[v.size() - 1];
v[v.size() - 1] -> right = v[0];
return v[0];
}
};