力扣 BFS

[力扣]1162. 地图分析

地图分析BFS

Posted by JinFei on April 10, 2020

题目描述

你现在手里有一份大小为 N x N 的「地图」（网格） grid，上面的每个「区域」（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，请你找出一个海洋区域，这个海洋区域到离它最近的陆地区域的距离是最大的。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 -  y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

Example1:

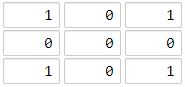  ![image](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/08/17/1336_ex1.jpeg)
    输入：[[1,0,1],[0,0,0],[1,0,1]]
    输出：2
    解释： 
    海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

Example2:

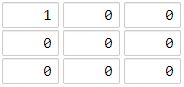  ![image](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/08/17/1336_ex2.jpeg)
    输入：[[1,0,0],[0,0,0],[0,0,0]]
    输出：4
    解释： 
    海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。

提示

1 <= grid.length == grid[0].length <= 100
grid[i][j] 不是 0 就是 1

解题思路

BFS
模版题参考
有一点，这里是从陆地开始的，初始距离应该是-1

由于BFS的第一层遍历是从陆地开始，因此遍历完第一层之后distance应该是0， -》所以初始化应该是-1

  BFS使用队列，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。BFS总共有两个模板：

  如果不需要确定当前遍历到了哪一层，BFS模板如下。
  while queue 不空：
      cur = queue.pop()
      for 节点 in cur的所有相邻节点：
          if 该节点有效且未访问过：
              queue.push(该节点)
  如果要确定当前遍历到了哪一层，BFS模板如下。
  这里增加了level表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size表示在当前遍历层有多少个元素，也     就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。
  level = 0
  while queue 不空：
      size = queue.size()
      while (size --) {
          cur = queue.pop()
          for 节点 in cur的所有相邻节点：
              if 该节点有效且未被访问过：
                  queue.push(该节点)
      }
  level ++;

class Solution {
public:
    int maxDistance(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        queue<pair<int, int>> q;
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                if(grid[i][j] == 1){
                    q.push(make_pair(i, j));
                }
            }
        }
        if(q.size() == 0 || q.size() == row * col){
            return -1;
        }
        int distance = -1;  // 陆地开始，应该是从-1开始
        
        while(!q.empty()){
            distance++;
            int size = q.size();
            for(int i = 0; i < size; i++){
                pair<int, int> t = q.front();
                q.pop();
                int r = t.first;
                int c = t.second;
                if(r - 1 >= 0 && grid[r - 1][c] == 0){
                    grid[r - 1][c] = 2;
                    q.push(make_pair(r - 1, c));
                }
                if(r + 1 < row && grid[r + 1][c] == 0){
                    grid[r + 1][c] = 2;
                    q.push(make_pair(r + 1, c));
                }
                if(c - 1 >= 0 && grid[r][c - 1] == 0){
                    grid[r][c - 1] = 2;
                    q.push(make_pair(r, c - 1));
                }
                if(c + 1 < col && grid[r][c + 1] == 0){
                    grid[r][c + 1] = 2;
                    q.push(make_pair(r, c + 1));
                }
            }
        }
        return distance;

    }
};